MAPAS DE CMAPTOOLS Y MIND MANAGER

                                

SOFTWARES EDUCATIVOS

          MINDMANAGER                         

MindManager, llamados MindMan, hasta la versión 3.5, es un programa comercial de mapas mentales (mind map por su descripción en inglés) desarrollado por Mindjet Corporation. Los mapas mentales creados en MindManager se basan en el método de mapeo de la mente por Tony Buzan. La última versión, MindManager 8, está disponible solamente paraMicrosoft Windows, aunque las versiones anteriores apoyadas Mac OS X y los archivos creados en las versiones más recientes son compatibles con ambas plataformas. En 2008 presentó Mindjet Connect, un servicio de colaboración en línea con el almacenamiento centralizado, Instant Meeting, y las características de comunicación. Connect es accesible con MindManager 8 en Windows y Web a través de MindManager, basado en un cliente de Flash.

Las características que se incluyen en el manual son para el soporte degestión de tareas, filtros, proceso abierto API, y el apoyo de RSS. Los mapas pueden extraer datos de Microsoft Excel y Outlook, y pueden ser exportados a Microsoft Word, PowerPoint, Visio y Project, así como a páginas web HTML y como a documentos en formato PDF.

HISTORIA:

 Línea de productos actual en negrita.

Fecha	Nombre y versión	Sistemas operativos soportados	Idiomas
1994	MindMan 1.0	Microsoft Windows	Inglés, Alemán
1996	MindMan 2.0	Microsoft Windows	Inglés, Alemán
1997	MindMan 3.0	Microsoft Windows	Inglés, Alemán
1998	MindManager 3.5	Microsoft Windows	Inglés, Alemán
1999	MindManager 4	Microsoft Windows	Inglés, Alemán
2000	MindManager 2002	Microsoft Windows	Inglés, Alemán.
2002	MindManager	PocketPC y PalmOS	Inglés, Alemán.
2003	MindManager forTablet PC	Microsoft Windows	Inglés, Alemán.
2003	MindManager X5	Microsoft Windows	Inglés, Alemán.
2005	MindManager 6	Microsoft Windows	Inglés, Alemán.
2006	MindManager 6	Microsoft Windows	Francés, Japonés.
2006	MindManager 6	Mac OS X	Inglés, Alemán, Francés, Japonés.
2007	MindManager 7	Microsoft Windows, Mac OS X	Inglés, Alemán, Francés, Japonés.
2008	Mindjet Connect	Microsoft Windows	Inglés, Alemán.
2008	MindManager Web	Todos (Adobe Flash)	Inglés, Alemán.
2008	MindManager 8	Microsoft Windows	Inglés, Alemán.
2010	MindManager 8	Mac OS X	Inglés.

Mind Manager es una aplicación con la que poder crear mapas mentales. Los mapas mentales son la forma sencilla de gestionar y ordenar las ideas que rondan nuestro cerebro plasmadas en forma de mapa.

Mind Manager provee una serie de plantillas acorde a diferentes situaciones (reuniones, listas de tareas, planificaciones semanales,...) para que sea más rápido y sencillo el comenzar a elaborar nuestros propios mapas. Su interfaz es sencilla y ya seamos usuarios noveles o avanzados adaptarnos al entorno de Mind Manager no resulta difícil.

Pero hay más, Mind Manager incluye una característica que me ha gustado y parece muy interesante: la integración con iCal. Gracias a ésta, podemos vincular eventos directamente con nuestro calendario, de esta forma irán apareciendo en nuestro mapa mental según vaya transcurriendo el día, semana o mes y los atributos especificados. Haciendo aun más efectiva la utilización del mapa como herramienta organizativa.

Sin duda una aplicación interesante que sólo tiene una pega, su precio. Y digo pega pero no es del todo cierto. Si eres un usuario cuya necesidad en realizar este tipo de mapas mentales es alta seguro que los 179 euros que cuesta su licencia es compensada. Si sólo vais a hacer un par de ellos mejor probar con otras alternativas gratuitas o más económicas.

 COMO USAR MIND MANAGERD:

SOFTWARES EDUCATIVOS

        CMAPTOOLS

                       

 QUÉ SON LOS CMAP TOOLS: 

  Es un software multiplataforma para crear mapas conceptuales, por medio de unas aplicaciones escritas en Java. Permite tanto el trabajo local individual, como en red, ya sea local, o en internet, con lo que facilita el trabajo en grupo o colaborativo.

Posibilita la navegación por los mapas realizados, lo que los convierte en interactivos. Se pueden enlazar e indexar prácticamente todo tipo de archivos, con la posibilidad de añadir información contextual a cada uno de los conceptos o nodos del mapa.

USO PEDAGÓGICO

  

  Puede describirse en cuatro momentos fundamentales:

1.La fase preparatoria

2.La material o materializada

3.La verbal

4.La mental

LA FASE PREPARATORIA

Carácter motivacional y de orientación de la actividad del alumno

Mapa conceptual como instrumento didáctico eficaz para presentar los contenidos del tema

Se les debe explicar las características de los mapas conceptuales, su utilidad para el procesamiento de la información, así como el procedimiento para construirlos.

LA MATERIAL O MATERIALIZADA

El estudiante debe interactuar con el objeto real o con su representación

El mapa conceptual como un medio didáctico para la materialización del objeto de estudio

LA VERBAL

Se caracteriza por el uso del lenguaje oral o escrito, los alumnos pueden construir grupalmente mapas conceptuales relacionados con el contenido, de manera que en la interacción exterioricen sus estructuras conceptuales individuales y negocien sus concepciones.

 LA MENTAL

  El estudiante debe ejecutar las tareas sin apoyo externo, Aquí el mapa construido puede ser un medio para evaluar el aprendizaje del estudiante.

  

cmaptools es una  herramienta   para  confeccionar esquemas conceptuales. el objetivo del programa  consiste en presentar gráficamente conceptos teóricos.

este  fin  lo lleva a cabo mediante una completa lista de recursos visuales que permiten vincular ideas de diferentes formas.

cmaptools dispone de un  acceso  vía  internet  a una ingente colección de trabajos que pueden servirnos como guía  para nuestro proyecto, o simplemente como  base que modificar para empezar a diseñar un mapa conceptual.

convertir los esquemas directamente en formato  web  es otra de las aportaciones realmente gratificantes de este programa, ya que facilita enormemente la publicación y difusión de los trabajos.

cmaptools es un programa realmente completo y útil. merece la pena invertir algo de tiempo en aprender a manejarlo.

descarga   gratis  cmaptools, en el siguiente link:

http://cmaptools.softonic.com/

CADENA DE SECUENCIAS

            CADENA DE SECUENCIAS:

La cadena de secuencias es un instrumento útil para representar cualquier serie de eventos que ocurre en orden cronológico o para mostrar las fases de un proceso.

En la escuela hay muchos contenidos para los cuales resultan aplicables las cadenas de secuencias; para citar algunos ejemplos: temas históricos, etapas de evolución de los seres vivos, secuencias narrativas (orden en que aparecen los eventos mas importantes en un cuento). Los usos en evaluación son similares a los explicados para las otras representaciones gráficas.

                             

DIAGRAMAS DE VENN

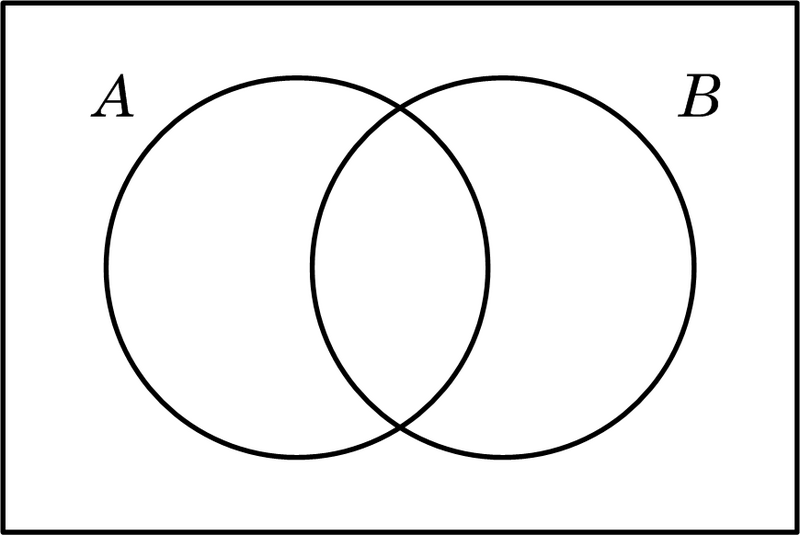
                            DIAGRAMAS DE VENN

Los diagramas de Venn son esquemas usados en la teoría de conjuntos, tema de interés en matemática, lógica de clases y razonamiento diagramático. Estos diagramas muestran colecciones (conjuntos) de cosas (elementos) por medio de líneas cerradas. La línea cerrada exterior abarca a todos los elementos bajo consideración, el conjunto universal U.

Con los diagramas de Venn es posible representar las relaciones de intersección, inclusión y disyunción sin cambiar la posición relativa de los conjuntos

Intersección:

Dado que los conjuntos pueden tener elementos comunes, las regiones encerradas por sus líneas límite se superponen. El conjunto de los elementos que pertenecen simultáneamente a otros dos es la intersección de ambos.¹

A = {1; 2; 3; 4; 6; 12}                                                       B = {1; 3; 5; 15}	z
A = {x | x es divisor natural de 12} B = {x | x es divisor natural de 15} U = {x | x es natural menor o igual que 16}

Inclusión:

Si todos los elementos de un conjunto son parte de los elementos de otro, se dice que el primero es un subconjunto del segundo o que está incluido en el segundo.¹ En los diagramas de Venn, todas las regiones de superposición posibles deben ser representadas. Y, cuando hay regiones que no contienen elementos (regiones vacías), la situación se indica anulándolas (con un color de fondo distinto).²

A = {1; 2; 3; 4; 6; 12} B = {1; 2; 3; 6} U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12}
A = {x | x es divisor natural de 12} B = {x | x es divisor natural de 6} U = {x | x es natural menor o igual que 12}

Disyunción:

Cuando los conjuntos no tienen elementos comunes, la región de superposición queda vacía.

A = {2; 4; 6; 8} B = {1; 3; 5; 7; 9} U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10}
A = {x | x es par y de una cifra} B = {x | x es impar y de una cifra} U = {x | x es natural menor o igual que 10}

A la izquierda de los diagramas, las definiciones de los conjuntos por enumeración y por comprensión.

ORIGEN E HISTORIA

Los diagramas de Venn tienen el nombre de su creador, John Venn, matemático y filósofo británico.³ Estudiante y más tarde profesor del Caius College de laUniversidad de Cambridge, Venn desarrolló toda su producción intelectual en ese ámbito.⁴

Los diagramas que hoy conocemos fueron presentados en julio de 1880 en el trabajo titulado De la representación mecánica y diagramática de proposiciones y razonamientos, que tuvo gran repercusión en el mundo de la lógica formal. Los diagramas de Venn tienen varios antecedentes. La primera representación gráfica de deducciones lógicas —y, en particular, de silogismos— se atribuye comúnmente a Gottfried Leibniz. Variantes de la misma fueron empleadas luego por George Boole y Augustus De Morgan, pero fue el gran matemático suizo Leonhard Eulerquien primero introdujo una notación clara y sencilla.² El siguiente diagrama muestra de otro modo la relación de inclusión del ejemplo dado en la introducción.

diagrama de Euler

Los diagramas de Euler se distinguen de los de Venn en dos aspectos:

• en ellos no aparecen las regiones vacías y
• el conjunto universal no se representa.

Si bien fue Venn quien introdujo la expresión "universo del discurso", él nunca representó al universal en sus trabajos.³ Por eso la idea de conjunto universal se atribuye habitualmente a Charles Dodgson, más conocido como Lewis Carroll, el lógico y autor de cuentos para niños que popularizó el concepto de conjunto complementario.¹ El conjunto universal fue cuestionado por Bertrand Russell, quien mostró que con tal concepto la teoría de conjuntos resultaba inconsistente (véase paradoja). Sin embargo, dicha definición fue rescatada y aun justificada en una reciente extensión de los diagramas de Venn que distingue al universal del Todo (universo del discurso).⁶ Por las dos razones recién mencionadas, los diagramas de Venn llegaron a convertirse en el nuevo estándar para la formalización de operaciones lógicas y los sistemas de representación anteriores cayeron en desuso.²

Tiempo después de la aparición del primer artículo, Venn desarrolló algo más su nuevo sistema en el libro Lógica simbólica, publicado en 1881 y cuyo propósito era interpretar y revisar los trabajos de Boole en el campo de la lógica formal. Este libro sirvió sobre todo para presentar ejemplos del uso de los diagramas.⁷ Otro libro de Venn que ayudó a divulgar el nuevo sistema de representación fue el titulado Los principios de la lógica empírica o inductiva, publicado en 1889.⁸

La primera constancia escrita del uso de la expresión "diagrama de Venn" es muy tardía (1918) y se encuentra en el libro A Survey of Symbolic Logic de Clarence Irving Lewis.

Diagramas de Venn de enunciados

Como se mostró en la introducción, los diagramas de Venn pueden ser definidos por enumeración de sus elementos o por indicación de una característica común que los identifica unívocamente.¹ De ahí que haya dos tipos de diagramas de Venn: los que muestran elementos reunidos por líneas cerradas y los que simplemente muestran enunciados o conceptos. Estos últimos son más interesantes porque permiten operar de manera abstracta y llegar a conclusiones más generales.

Los siguientes diagramas del segundo tipo muestran los resultados de cuatro operaciones básicas con conjuntos usando el código del semáforo de dos colores.

¬A	A ∧ B	A ∨ B = ¬((¬A) ∧ (¬B))	A – B = A ∧ (¬B)

Como se desprende de las igualdades, con las dos primeras operaciones (negación y conjunción), es posible hacer las otras dos (disyunción y sustracción).

El código de dos colores puede ser interpretado en el sistema binario de numeración: rojo = 0; verde = 1. A los resultados de las operaciones se los puede entonces digitalizar. Y a los términos que participan de las operaciones, también. De este modo, las operaciones con conjuntos se convierten en operaciones con números.

Diagramas de Venn y cantidad de definiciones

Los siguientes diagramas muestran la cantidad de regiones en que queda dividido el conjunto universal con una, dos y tres definiciones.

1 conjunto (2 colores)	2 conjuntos (4 colores)	3 conjuntos (8 colores)

Entre los colores se cuenta el gris, que en todos los casos corresponde a los elementos que no caen en ninguna definición.

DIAGRAMA DE UN CONJUNTO

Tiene sólo 2 regiones: la de los elementos que responden a la definición A y la de los que se oponen a ella.¹

DIAGRAMA DE DOS CONJUNTOS

Tiene 4 regiones. Considérese el siguiente ejemplo: el conjunto A es el de los animales bípedos y el conjunto B es el de los animales que pueden volar. El área donde las dos regiones se superponen contiene por lo tanto a todos los animales que, al mismo tiempo, son bípedos y pueden volar. En resumen:

• A (regiones amarilla y verde): animales bípedos,
• B (regiones azul y verde): animales que pueden volar,
• A y B (región verde): animales bípedos que pueden volar,
• A y no B (región amarilla): animales bípedos que no pueden volar,
• no A y B (región azul): animales no bípedos (que no tienen dos patas) que pueden volar,
• no A y no B (región gris): animales no bípedos que no pueden volar,
• A o B (regiones amarilla, azul y verde): animales bípedos o que pueden volar.

Los pingüinos, que tienen dos patas y no pueden volar, están en la región amarilla; los mosquitos, que tienen seis patas y pueden volar, están en la región azul; los loros, que tienen dos patas y pueden volar, están en la región verde; las ballenas, que no tienen patas ni pueden volar, están en la región gris.

DIAGRAMA DE TRES CONJUNTOS

Tienen 8 regiones. Los diagramas de tres conjuntos fueron los más usados por Venn en toda su obra. Un ejemplo de aplicación podría ser el siguiente: dado un grupo de personas, A es el conjunto de las de sexo masculino, B el conjunto de las mayores de 18 años y C el conjunto de las que trabajan. De este modo, la región verde sería la de las personas de sexo masculino, mayores de 18 años, que no trabajan.

DIAGRAMAS DE MÁS DE TRES CONJUNTOS

La dificultad de representar más de tres conjuntos mediante diagramas de Venn es evidente. Venn sentía afición por los diagramas de más de tres conjuntos, a los que definía como "figuras simétricas, elegantes en sí mismas". A lo largo de su vida, diseñó varias representaciones usando elipses, y dejó indicaciones para la construcción de diagramas con cualquier cantidad de curvas, partiendo del diagrama de tres círculos.

DIAGRAMAS DE EDWARDS

Anthony William Fairbank Edwards propuso diagramas para más de tres conjuntos, proyectando el diagrama sobre una esfera. Tres conjuntos pueden ser representados fácilmente tomando tres hemisferios en ángulos rectos (x = 0, y = 0 y z = 0). Un cuarto conjunto puede ser representado tomando una curva similar a la juntura de una pelota de tenis que suba y baje alrededor del ecuador. Los conjuntos resultantes pueden ser proyectados de nuevo sobre el plano para mostrar diagramas de tipo engranaje, con cantidades cada vez mayores de dientes. Edwards ideó estos diagramas mientras diseñaba la ventana acristalada en memoria de Venn que hoy adorna el comedor del Caius College.¹⁵

Otros diagramas

Los diagramas de Edwards son topológicamente equivalentes a los diagramas diseñados por Branko Grünbaum, que se basan en la intersección de polígonos con cantidades crecientes de lados.^16 17 18 Phillip Smith ideó diagramas similares den conjuntos usando curvas senoidales con ecuaciones del tipo y = sen(2ⁱ x)/2ⁱ, 0 ≤ i ≤ n – 2. Por su parte, Lewis Carrolldiseñó un diagrama de cinco conjuntos.

                  

DIAGRAMAS DE VENN: